
Stack (堆疊) 和 queue (佇列) 可以說是 array 和 linked-list 的閹割版本,因此個別都可以用 array 和 linked-list 來實現。
1. Stack (堆疊)
1.1 定義與特性
Stack 也是 linear data structure 的一種,和 array 與 linked-list 最大的不同點是:
- 在 stack 中新增元素只有 push 這個 method,且會在 stack 的末端新增元素
- 在 stack 中刪除元素只有 pop 這個 method,且會在 stack 的末端刪除元素
- 因為只有以上這兩個 method 可以對 stack 做操作,因此在 stack 中最重要的特性為: LIFO - Last In First Out (後進先出)
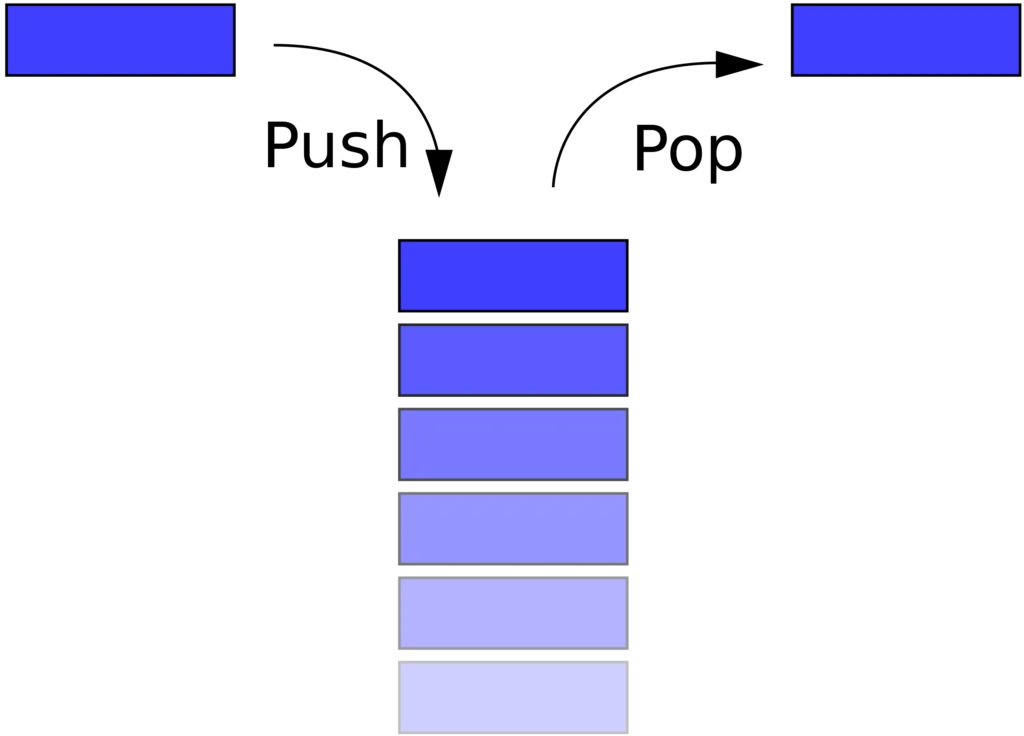
▲ 圖片來源:維基百科
可能有些人會問,既然 stack 只是 array 和 linked-list 的閹割版,那為什麼不直接使用 array 或 linked-list 就好了?這是為了在某些應用情況下「聚焦」需要解決的問題,例如:瀏覽器的瀏覽紀錄,雖然用 linked-list 也可以實現,但用 stack 可以聚焦在操作瀏覽紀錄的行為:後進先出的行為。
誠如文章開頭提到的,stack 和 queue 都可以用 array 和 linked-list 來實作,因此嚴格來說 stack 和 queue 都可以按照儲存結構分為
- 循序儲存結構 (用 array 實作)
- 鏈式儲存結構 (用 linked-list 實作)
用 array 實作的 stack 和 queue 有類似的特性:長度固定,不過可以用一些 method 來動態調整長度。用 linked-list 實作的 stack 和 queue 則是每一個資料節點都含有 pointer。
但因為 JavaScript 的 array 只有一種,因此以下就直接用 JavaScript 的 array 來實作 stack 和 queue,如果想知道如何用 array 和 linked-list 來實作 stack 和 queue,可以參考以下文章 (用 C++ 實作的):
[Stack: 以Array與Linked list實作](以Array與Linked list實作)
Queue: Intro(簡介),並以Linked list實作
Queue: 以Array實作Queue
1.2 時間複雜度
對 stack CRUD 的 time complexity (Average)
| Access | Search | Insertion | Deletion |
|---|---|---|---|
| O(n) | O(n) | O(1) | O(1) |
1.3 JavaScript 實作
class Stack {
constructor() {
this.data = [];
}
push(record) {
this.data.push(record);
}
pop() {
return this.data.pop();
}
peek() {
return this.data[this.data.length - 1];
}
isEmpty() {
return this.data.length === 0;
}
clear() {
this.data = [];
}
size() {
return this.data.length;
}
}2. Queue (佇列)
2.1 定義與特性
Queue 可以說是 stack 的兄弟,和 stack 有類似的屬性:
- 在 queue 中新增元素只有 enqueue 這個 method,且會在 queue 的首端新增元素
- 在 queue 中刪除元素只有 dequeue 這個 method,且會在 queue 的末端刪除元素
- 因為只有以上這兩個 method 可以對 queue 做操作,因此在 queue 中最重要的特性為: FIFO - First In First Out (先進先出)
可以觀察到和 stack 最大的差別就是在新增元素的時候,stack 是在末端新增元素 (對應到 JavaScript 的 Array.prototype.push()),queue 則是在首端新增元素 (對應到 JavaScript 的 Array.prototype.unshift())。
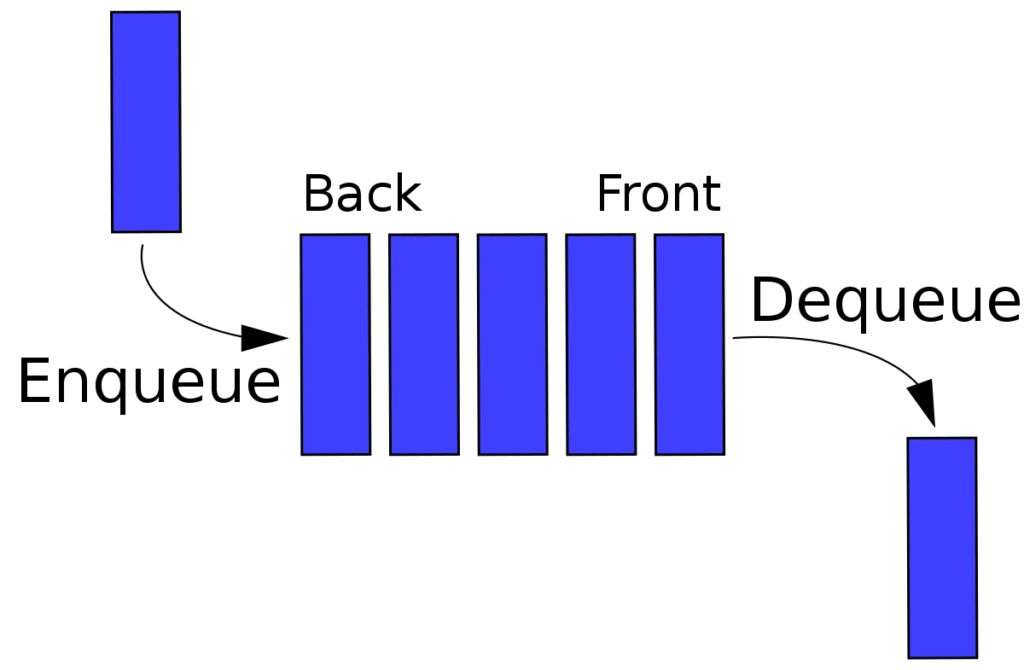
▲ 圖片來源:維基百科
2.2 時間複雜度
對 queue CRUD 的 time complexity (Average)
| Access | Search | Insertion | Deletion |
|---|---|---|---|
| O(n) | O(n) | O(1) | O(1) |
2.3 JavaScript 實作
class Queue {
constructor() {
this.data = [];
}
enqueue(record) {
this.data.unshift(record);
}
dequeue() {
return this.data.pop();
}
getFront() {
return this.data[0];
}
getBack() {
return this.data[this.data.length - 1];
}
isEmpty() {
return this.data.length === 0;
}
clear() {
this.data = [];
}
size() {
return this.data.length;
}
}3. 參考資料
大話資料結構(全新彩色版)
[Stack: 以Array與Linked list實作](%E4%BB%A5Array%E8%88%87Linked list%E5%AF%A6%E4%BD%9C)
Queue: Intro(簡介),並以Linked list實作
Queue: 以Array實作Queue


