資料結構筆記 3

1. 定義與特性

1.1 定義

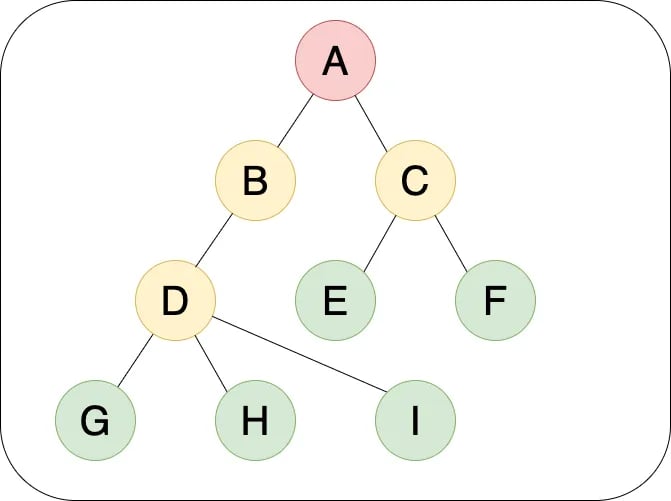
Tree 是最常見的 non-linear data structure，構成 tree 的基本單位為 node，以下為 tree 的定義：

Root Node：(根節點)為 tree 的起點，每一個 tree 僅有一個且唯一的 root node
- A 為 root node
SubTree：每個 node 底下可以分為互不相交的有限集合，稱為 subTree，以下用 T 來表示
- A 有兩個 subTree: T1(B, D, G, H, I)、T2(C, E, F)
- B 有一個 subTree: T1(D, G, H, I)
- C 有兩個 subTree: T1(E)、T2(F)
- D 有三個 subTree: T1(G)、T2(H)、T3(I)

1.2 特性

n 為 tree 中的 node 數，任一 n > 0 的 tree 有以下的特性：

tree

Degree：每個 node 擁有的 subTree 個數稱為 degree
- A 的 degree = 2
- B 的 degree = 1
- C 的 degree = 2
- D 的 degree = 3
Leaf Node / External Node：degree = 0 的 node 稱為 leaf node (葉節點) 或 external node (外部節點)
- E, F, G, H, I 為 leaf node 亦為 external node
Internal Node：degree >= 1 的 node 稱為 internal node (內部節點)
- B, C, D 為 internal node
Child Node：node 的 subTree 的 root node 稱為該 node 的 child node
- B, C 為 A 的 child node
- D 為 B 的 child node
- G, H, I 為 D 的 child node
- E, F 為 C 的 child node
Parent Node：node 的 subTree 的 root node 稱該 node 為 parent node
- A 為 B, C 的 parent node
- B 為 D 的 parent node
- D 為 G, H, I 的 parent node
- C 為 E, F 的 parent node
Siblings：parent node 一樣的 node 稱為 siblings
- B, C 為彼此的 siblings
- G, H, I 為彼此的 siblings
- E, F 為彼此的 siblings
Ancestor Node：某個 node 到 root node 路徑上的任意 node 皆為該 node 的 ancestor node
- A, B, D 為 G 的 ancestor node
- A, C 為 E 的 ancestor node
Descendant Node：某個 node 的 subTree 上的所有節點皆為該 node 的 descendant node
- A 的 descendant node 為此 tree 中的所有 node (除了 A)
- B 的 descendant node 為 D, G, H, I
- C 的 descendant node 為 E, F
Level：node 的 level 從 root node 定義起，root node 的 level 為 1，其 child 的 level 為 2，以此類推
- A 的 level = 1
- B, C 的 level = 2
- D, E, F 的 level = 3
- G, H, I 的 level = 4
Depth：depth 為某個 node 到 root node 的距離
- B, C 的 depth = 1
- D, E, F 的 depth = 2
- G, H, I 的 depth = 3
- 此 tree 的 depth = 3
Height：height 為某個 node 到 leaf node 的距離
- B 的 height = 2
- D 的 height = 1
- A height = 3
- 此 tree 的 height = 3

2. JavaScript 實作

2.1 Node

class Node {
  constructor(data) {
    this.data = data;
    this.children = [];
  }
  add(data) {
    this.children.push(new Node(data));
  }
  remove(data) {
    this.children = this.children.filter(node => node.data !== data);
  }
}

2.2 Tree

2.2.1 建立 tree

以此圖為例，建立該 tree：

tree

class Tree {
  constructor() {
    this.root = null;
  }
}

const t = new Tree();
t.root = new Node('A');
t.root.add('B');
t.root.add('C');
t.root.children[0].add('D');
t.root.children[0].children[0].add('G');
t.root.children[0].children[0].add('H');
t.root.children[0].children[0].add('I');
t.root.children[1].add('E');
t.root.children[1].add('F');

通常 tree 裡面會有兩個 method 用來存取 (遍歷) tree 中的每個節點，稱為 traversal (走訪)。

2.2.2 BFS - Breadth-first Search (廣度優先搜尋)

廣度優先，就是會先訪問一樣深度的 (也就是一樣廣度的 node ) 後，再往更深的深度訪問。以下圖為例，遍歷的順序為：A, B, C, D, E, F, G, H, I。

tree

traverseBF(fn) {
  const arr = [this.root];
  while (arr.length) {
    const node = arr.shift();
    arr.push(...node.children);
    fn(node);
  }
}

2.2.3 DFS - Depth-first Search (深度優先搜尋)

深度優先會由左至右訪問最深的 node 後，再往右側的 node 訪問，以下圖的 tree 為例，訪問的順序為：A, B, D, G, H, I, C, E, F。

tree

traverseDF(fn) {
  const arr = [this.root];
  while (arr.length) {
    const node = arr.shift();
    arr.unshift(...node.children);
    fn(node);
  }
}

完整的 code：

class Tree {
  constructor() {
    this.root = null;
  }

  traverseBF(fn) {
    const arr = [this.root];
    while (arr.length) {
      const node = arr.shift();
      arr.push(...node.children);
      fn(node);
    }
  }

  traverseDF(fn) {
    const arr = [this.root];
    while (arr.length) {
      const node = arr.shift();
      arr.unshift(...node.children);
      fn(node);
    }
  }
}

// Building a tree
const t = new Tree();
t.root = new Node('A');
t.root.add('B');
t.root.add('C');
t.root.children[0].add('D');
t.root.children[0].children[0].add('G');
t.root.children[0].children[0].add('H');
t.root.children[0].children[0].add('I');
t.root.children[1].add('E');
t.root.children[1].add('F');

// Traverse the tree
const lettersBF = [];
const lettersDF = [];
t.traverseBF(node => {
  lettersBF.push(node.data);
});

t.traverseDF(node => {
  lettersDF.push(node.data);
})

console.log(lettersBF);
 /*
[
  'A', 'B', 'C',
  'D', 'E', 'F',
  'G', 'H', 'I'
]
*/
console.log(lettersDF);
/*
[
  'A', 'B', 'D',
  'G', 'H', 'I',
  'C', 'E', 'F'
]
*/