Selection sort 的原理如其名：每次找出最小的元素，如果找得到比現在最小的元素還小的，就和尚未排序好的最左邊元素交換，找不到則不執行動作。

1. Selection Sort 原理解釋

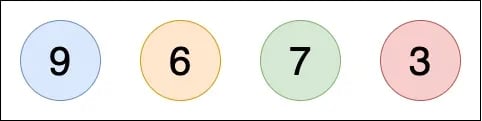
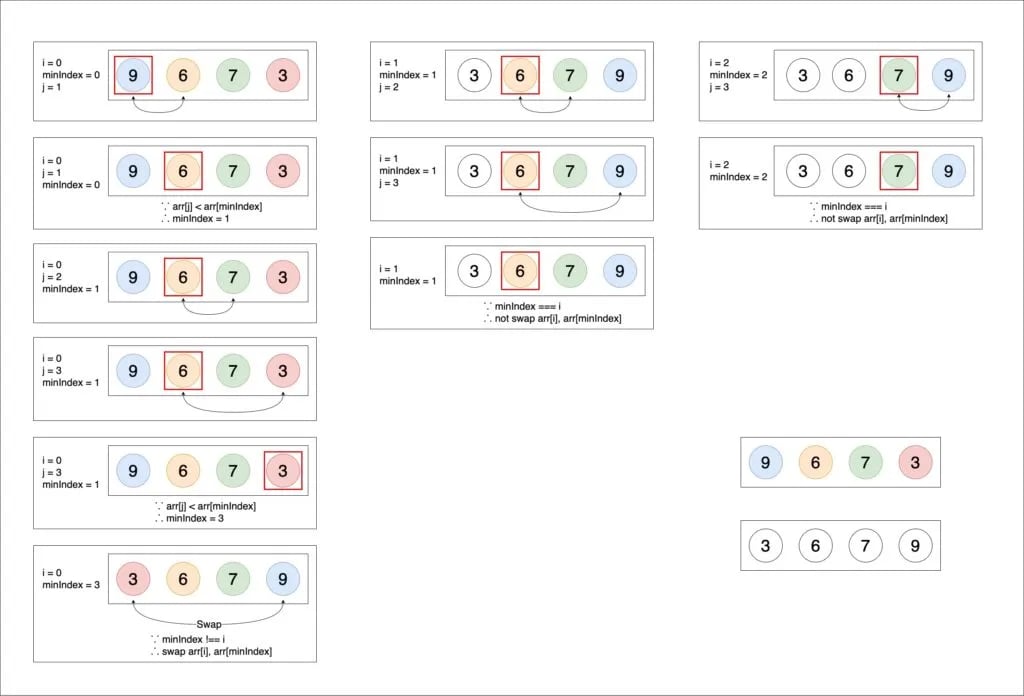
首先將最小元素的 index 假設為第一個元素，接著一個個和後面元素相比，第一輪 (i = 0)：

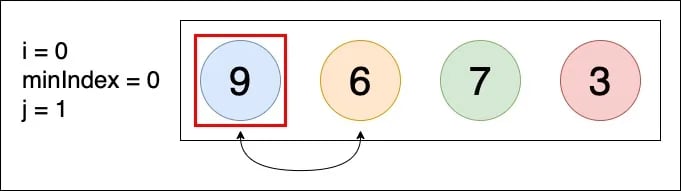
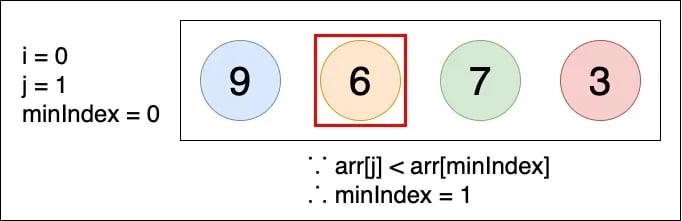
▲ arr[minIndex] 和 arr[j] 相比，因為 6 < 9，因此將 minIndex 從 0 變為 j (j = 1)

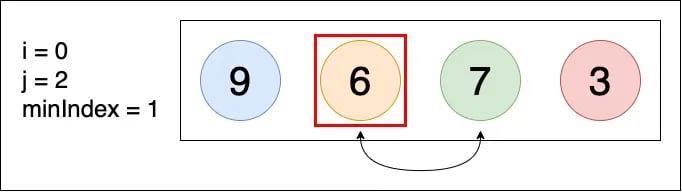
▲ arr[minIndex] 和 arr[j] 相比，因為 6 < 7，所以 minIndex 維持不變

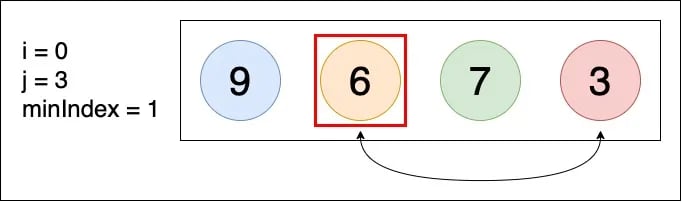
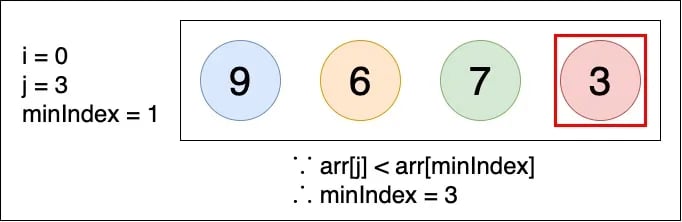
▲ arr[minIndex] 和 arr[j] 相比，因為 3 < 7，因此將 minIndex 從 1 變為 j (j = 3)

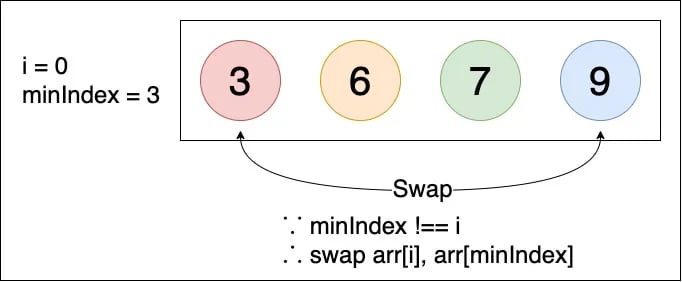
▲ 在第一輪結束前則要確認一開始的假設 (minIndex = i) 是否正確，因為現在的 minIndex = 3，因此需要 arr[i] 需要和 arr[minIndex] 位置對調

接著第二輪 (i = 1)，邏輯和剛剛的第一輪類似，arr[j] 和 arr[minIndex] 不停比較，若順序錯誤則將 minIndex 重新賦值為 j：

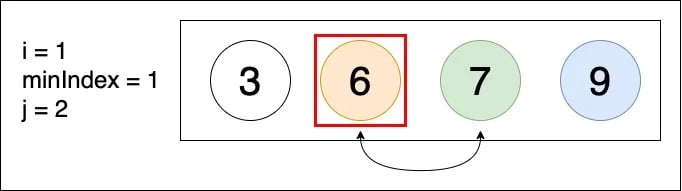
▲ arr[minIndex] < arr[j]，故 minIndex 的值維持不變

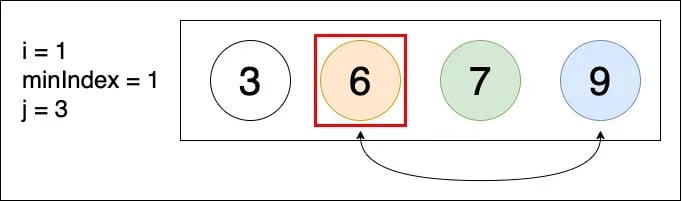
▲ arr[minIndex] < arr[j]，故 minIndex 的值維持不變

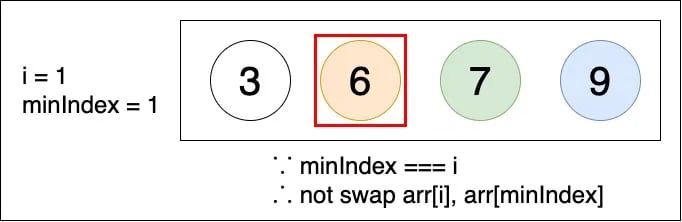
第二輪結束前，確認一開始的假設是否正確，在這一輪中 minIndex 一樣是 i，因此不需要將 arr[i] 和 arr[minIndex] 對調

第三輪 (i = 2)：

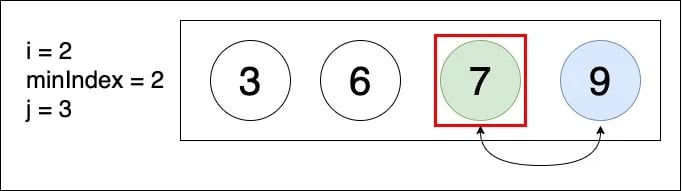
▲ arr[minIndex] < arr[j]，因此 minIndex 維持不變

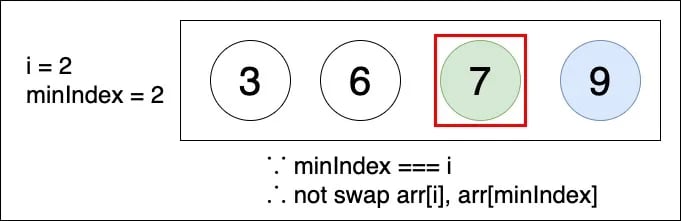
▲ 和第二輪一樣，minIndex === i，因此不需對調 arr[i] 和 arr[minIndex]

2. JavaScript 實作

function selectionSort(arr) {
  const n = arr.length;
  for (let i = 0; i < n - 1; i++) {
    let minIndex = i;
    for (let j = i + 1; j < n; j++) {
      if (arr[j] < arr[minIndex]) {
        minIndex = j;
      }
    }
    if (minIndex !== i) {
      const temp = arr[minIndex];
      arr[minIndex] = arr[i];
      arr[i] = temp;
      // [arr[minIndex], arr[i]] = [arr[i], arr[minIndex]];
    }
  }
  return arr;
}

概念圖：

3. Time Complexity

最佳：O(n2)
最差：O(n2)
平均：O(n2)

4. 參考資料

大話資料結構(全新彩色版)
The Coding Interview Bootcamp: Algorithms + Data Structures